

The Red Queen -- Alice Through The Looking Glass
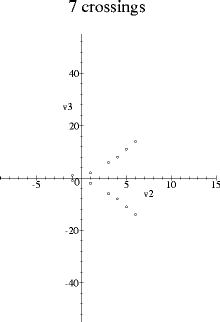
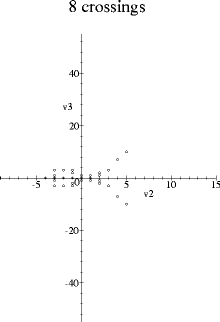
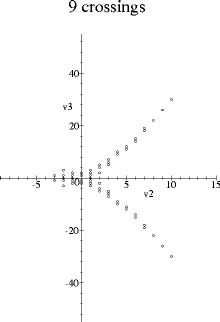
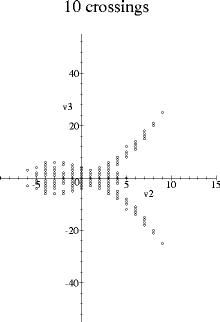
The following graphs were obtained by plotting the first two additive Vassiliev knot invariants against each other for all prime knots with a given crossing number. The data for knots up to ten crossings are from Stanford's list of Vassiliev invariants up to degree six, and the eleven and twelve crossing knots were calculated from Thistlethwaite's table of Jones polynomials.
These pictures appeared first in my thesis and are also in the paper On the first two Vassiliev invariants, where I also plot the thirteen and fourteen crossing knots (the pattern continues).
Both v2 and v3 are normalized so that they take value one on the positive trefoil. v2 is the unique such additive type two invariant, and v3 is the unique such additive type three invariant which multiplies by -1 under the mirror image map. (Another way of saying this is that the space of additive type three invariants has been decomposed into its +1 and its -1 eigenspaces with respect to the mirror image map.) So the symmetry in the x-axis seen in the pictures just corresponds to taking the mirror image of knots.
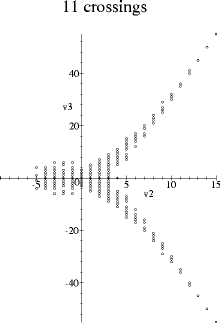
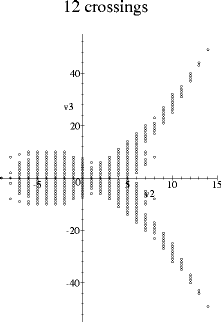
Mail me with your conjectures (or theorems) for the behaviour at higher crossing numbers.
Back to my home-page.