a. b.
b.
Simon Willerton
[Nature 368 103-104, 10 March 1994]
A CENTURY ago, physicists such as Lord Kelvin' first delved into the theory of knots in an attempt to explain the Periodic Table, the idea at the time being that knots represented some form of stability, and that joining two knots could represent the fusing of atoms. When this got nowhere, knot theory was left as an esoteric subject of study for pure mathematicians. But unexpected discoveries led to a renaissance in the 1980s; explanations for these have been trickling in from various areas, one being singularity theory, a branch of abstract mathematics, and another being quantum physics, where knots on the subatomic level were once again being considered. These two approaches have now been synthesized by Bar-Natan in a paper [2] to appear in Topology.
a. b.
b.
FIG. la, The (right) trefoil knot. This has Jones polynomial
x+x3-x4.
b, A knot with a double point or self-intersection.
Mathematicians consider an abstraction of a knot in a piece of string that has had its ends joined to stop it being untied, so a knot is a knotted circle in three-dimensional space that does not intersect itself (Fig.la). The study of knots is part of topology, the mathematical discipline in which shapes can be deformed in any way provided that they don't tear. Two knots are said to be of the same knot type if one can be deformed into the shape of the other.
But how do mathematicians tackle such problems as "Make a list (albeit infinite) of all of the possible types of knots" and "Determine (by a finite algorithm) whether two knots are of same type"? One approach is to study knot invariants, which assign to each knot a more tractable mathematical object, say a polynomial or a number, that is the same when evaluated on two knots of the same type. (A particular invariant may have the same value on two knots of different type.)
Until the mid-1980s, most knot invariants were derived from well understood topological ideas, but then an important invariant, the Jones polynomia1 [4], was defined combinatorially (in other words, one draws a two-dimensional picture of the knot, then uses an algorithm to cut it into sections and thus obtain the invariant. The final step is to show that it doesn't matter what drawing was originally taken). This is a powerful invariant, in that it is good at distinguishing between knots, but at the time it lacked the topological description required if it was to be placed in a more natural context, alongside previous invariants.
Evidently, a fresh approach was needed. Vassiliev [5], a specialist in singularity theory working in Moscow, looked at knots not as knotted circles in three-dimensional space, but as points in the abstract space of all knots. Analogously, consider a quadratic function: this can be thought of as a 'u' or 'n' shaped graph, or as being defined by the equation f(x) = ax2+bx+c, where a, b and c are real numbers. So each such function can be thought of as the point (a,b,c) in the space of all quadratics. The u-shaped graphs correspond to the triples (a,b,c) with a > 0 and the n-shaped graphs a < 0. These two regions are separated by a 'wall' - the plane a = 0, corresponding to functions with straight-line graphs.
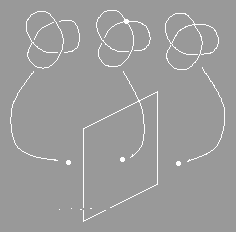
FIG. 2 A section of wall in knot space. On the right we have the trefoill knot, on the wall we have a knot with a doublepoint and on the left a 'knot' which is unknotted. Notice how in passing through the wall we push one strand of the knot through another.
Similarly, a knot corresponds to a point in the space of all knots. But whereas the function space was three-dimensional in the quadratic case, the space of all knots has infinite dimensions, making it (to put it mildly) harder to visualize. In this space the different knot types are separated into chambers by walls, the walls consisting of knots that have a self-intersection or 'double point' (Figs lb and 2 show examples). The walls meet at 'corners' which correspond to knots with two self-intersections. This analysis of walls and corners then generalizes to knots with a greater number of self-intersections. Vassiliev approached the study of these walls by studying numerical knot invariants (invariants that assign a number to every knot, and thus a single number to each 'chamber' described above). Such an invariant can be extended to knots with a single self-intersection - in other words, its value can be defined on the walls - by looking at the knots on either side of the wall. The number on the wall is simply the difference between the values on either side. Then this procedure can be extended to knots with two double points and so on. Vassiliev invariants are those invariants that are zero when extended to knots with a certain (large) number of double points. These invariants are quite simple to understand from certain viewpoints, and Birrnan and Lin [6] proved that the Jones polynomial is built up from invariants of this type.
The other approach was from quantum physics where one considers the probability of events happening: the probability of 'observables' such as the position and momentum of particles taking certain values. Around the mid-1980s physicists started considering space-times with no notion of distance. Think of two points marked on a rubber sheet: it is impossible to define a distance between the points, as stretching the sheet would alter the distance. Without the notion of distance, position and momentum become meaningless, so one needs topological ways of describing the motion of particles: in fact the only sensible thing to consider as an observable is the knottedness of the particles' trajectories.
A tool known as the Feynman path integral can be used to calculate the probabilities of particles traversing knot in three-dimensional space-time, thes probabilities depending only on the type of knot involved. A near-miraculous discovery was made by Witten', a physicist at Princeton, when he was able to construct a model for space-time in which this probabilistic invariant generalized the Jones polynomial. However, although physicists happily use the Feynman integral (as it seems to give them sensible answers), it has never been properly defined mathematically. A more rigorous analysis of Witten's construction has been sorely needed.
And this is where Bar-Natan's work comes in. Working under Witten, Bar-Natan [2,8] used perturbative methods to expand the Witten integral as a sum of terms that are easily understood mathematically, rather like expanding ex as powers of x. This expansion is in terms of generalized Feynman diagrams (see Fig. 3); the integral describes all possible ways that the particle can behave, and each Feynman chord diagram corresponds to one of these types of behaviour. Bar-Natan has shown that the invariant derived from each chord diagram is a Vassiliev invariant, neatly uniting the two topological approaches.
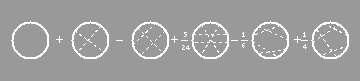
FIG. 3 The first six terms in an expansion of the trefoil knot in terms of chord diagrams. Each chord shows which parts of the circle are joined at double points (imagine shrinking the chord until the sides of the circle meet at its centre).
Where next for the knot theorists? Kontsevich [9] has constructed an integral that expands every knot as a sum of chord diagrams, and has proved that these methods give rise to all invariants of Vassiliev's type. His integral was originally impossible to calculate except for the simplest knots, but mathematicians are now finding ways of making it more calculable. So the latest results, although they have not answered every question, have certainly increased the arsenal with which knot theorists can attack their favourite tangles.