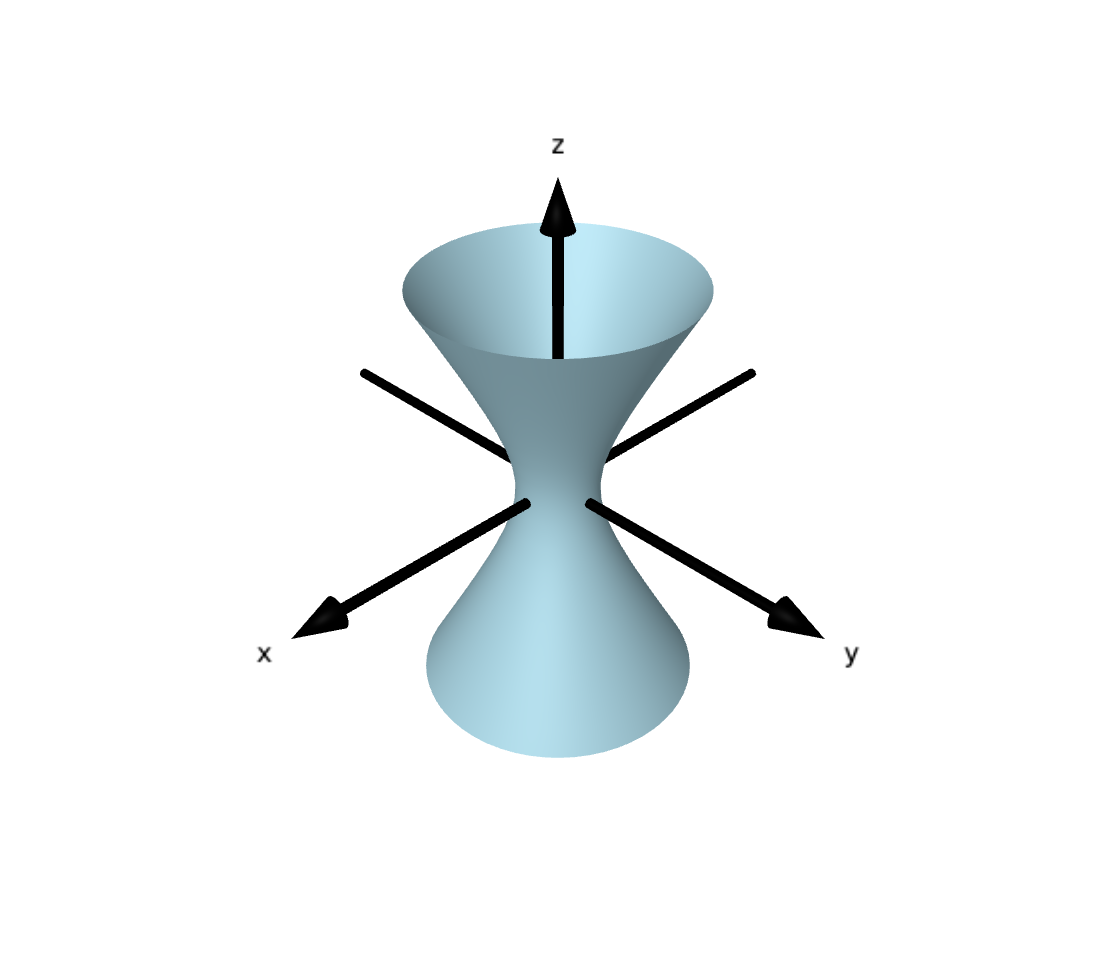
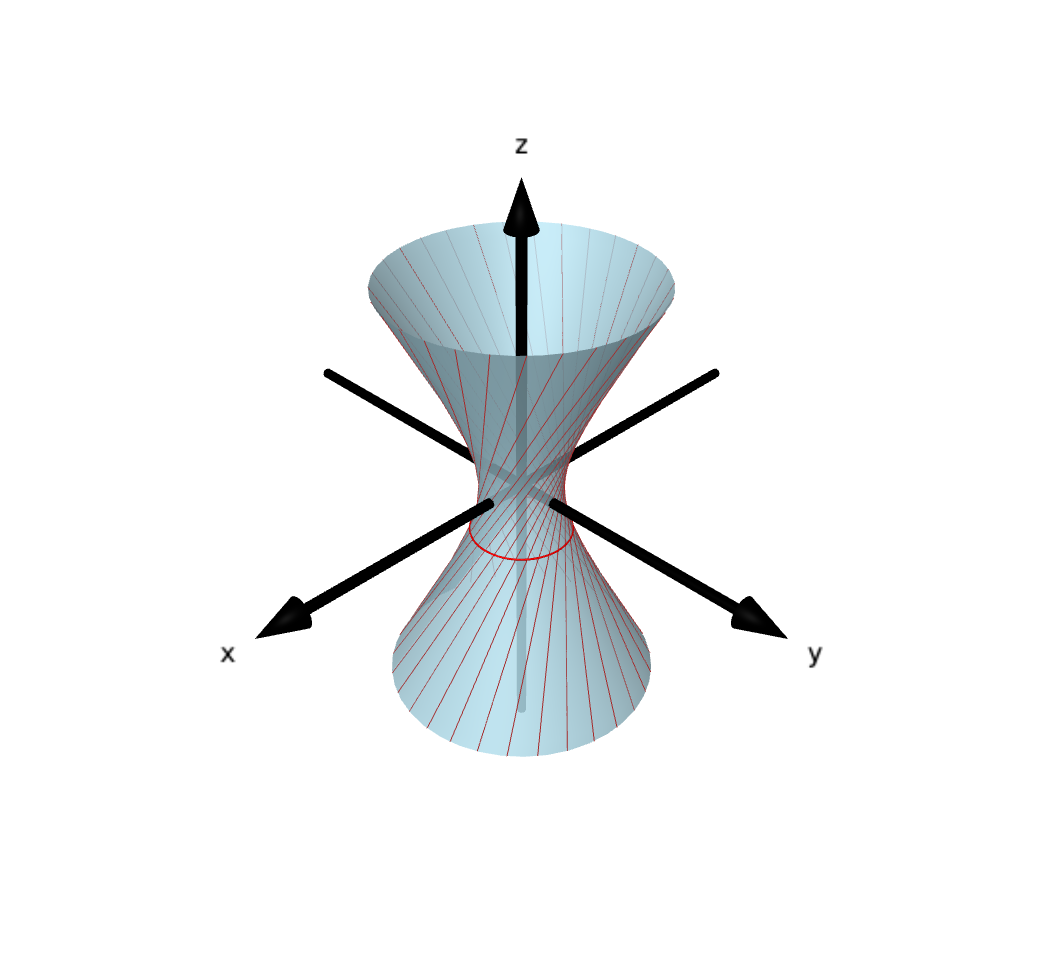
Animation examples
The curvature of a plane curve
We can consider the curve t ↦ (cos(5t), sin(3t)) for t a real number. Here's a plot of the curve and it's curvature.
Note that the curve is not unit speed; note how it slows down round the corners. Let's illustrate that by plotting the tangent vector on the curve, and also plotting the speed (ie. the magnitude of the tangent vector.
As that is not a unit-speed parametrization, the rotation of the tangent vector will not relate to the curvature. However, we can reparametrize to a unit-speed curve.
We now trace out the reparametrized curve with the tangent vector (which is necessarily a unit vector!) to see how the rotation speed of the tangent vector gives the curvature of the curve.
Going from cylinder to cone via hyperboloids
There's also the following interacrive webpages where you can move around the above animation. Note that the left hand animation is about 10MB and the right-hand one is 45MB!